有限自动机
的互相转换
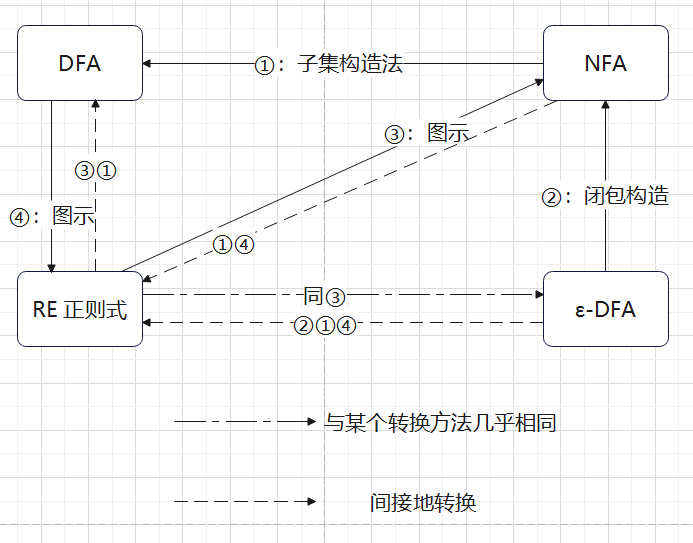
① P49:NFA转DFA
T:不变
Q及:从NFA的初始状态开始,将某个状态q接受某个字符x所可能转移到的状态合并到一个状态中,作为DFA的Q中一个新状态,这个转移规则作为的一项
F:构造完上述步骤之后,遍历DFA的Q,只要含有NFA的F中任意一个的状态,都是DFA的F
如:经a可能得,经b得,则构造状态、加入到DFA的状态。然后再对中的两个状态分别使用字符a进行推断,将得到的状态如放在一起作为一个新的状态。如此循环,直至不再出现新的状态。而NFA的终结状态为,则只要含有状态,就是DFA的终结状态
例:
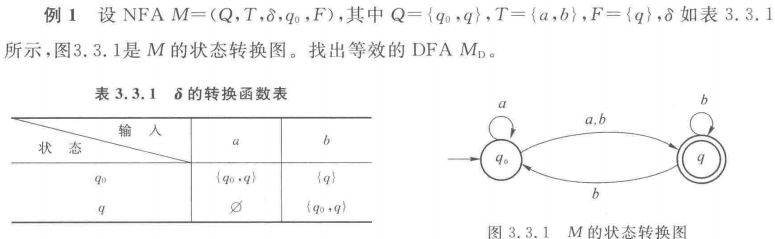

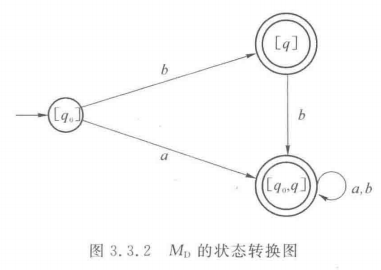
② P54:转NFA
: 若的闭包包含了原本F里的任意状态,则为 F并,否则就是原本的F
Q、T、:不变
:重点。
对于某一条转换规则,
-
(在原先的-NFA中)先去寻找的,
-
然后对这个闭包里的每一个状态都输入字符a(有可能某个状态不接受a,那么它的转换结果就是空集,不写出来),
-
再把得到的这个状态集里的每一个状态都求一遍,结果取并集,
-
然后对原先所有的都走如上的流程,就得到新的。
更直观的描述就是把不接受任何字符就能达到的状态作为起始(取第一个),然后用他去接收字符a(推一步),然后把结果状态及其空转换的状态作为结果(取第二个)
例:
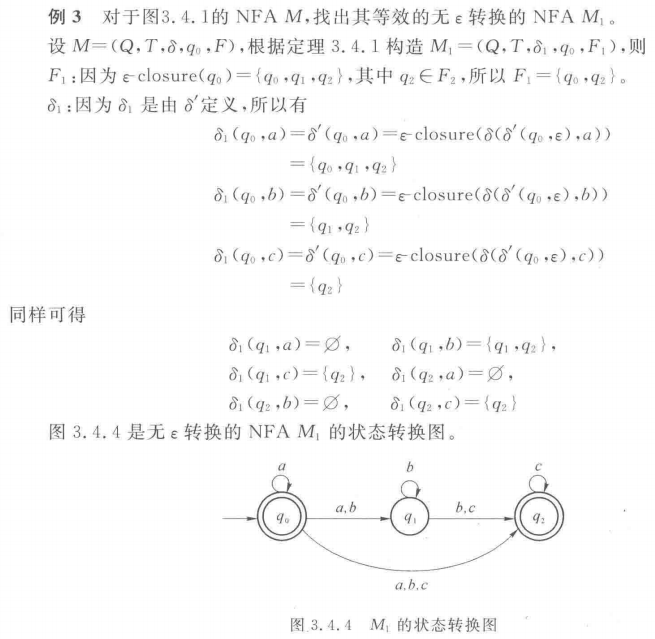
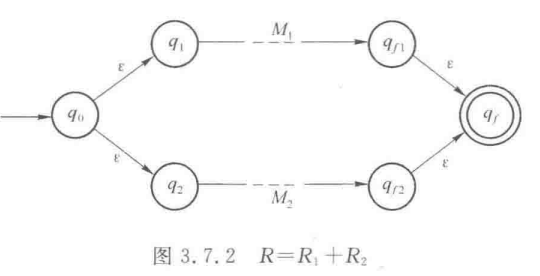
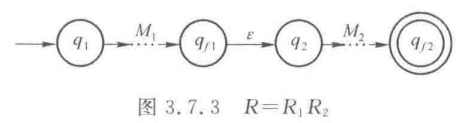
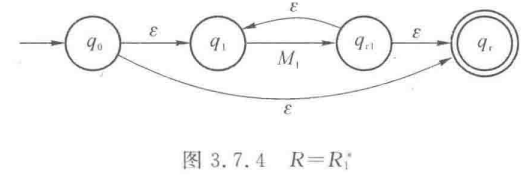
③ P60:RE转NFA
根据如下三种规则构造即可
值得一提的是,此处图中构造的是,如果不特别要求的话,完全可以直接构造NFA,此时还能大大化简上图(比如,可以只有的两部分)
④ P62:DFA构造正则式
首先对于每一个终态q,化简初态到q的路径上的状态(这里只关注到特定q的路径,路上的某个状态是不是可以去另外的某个终态是不关心的,可以当它那条边不存在)
将③中的规则逆过来即可
概括性的,如(糊了,是左上角的到右上角的状态)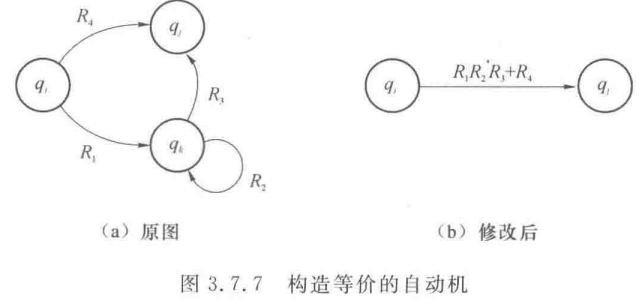
化简到类似下图(a)的形式,套公式构造即可
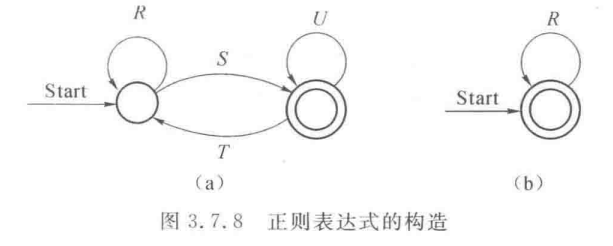
- 形如(a)的,表示为
- 形如(b)的,表示为
至此,以上四者的相互转换就完成了,一些没有列出的途径可以多用几次上述来间接的完成,比如从NFA得到一个正则式,可以先走①变成DFA,然后走④变成正则式——当然,如果熟练也可以直接完成转换,这里是纯粹只用书上讲过的方法来完成
加入文法的转换
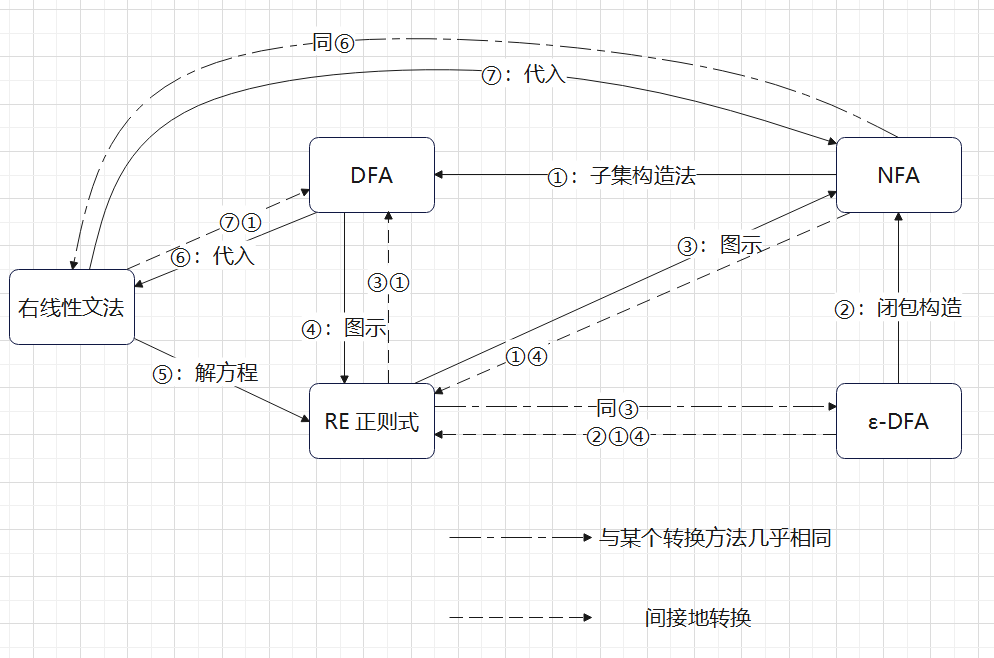
⑤ P56:右线性文法转RE
直接带入公式即可
唯一需要注意的一点是,一定要,不要看到就直接带入公式了。得要都是相同的非终结符,不能一个是S一个是A,那样子的不能用这个。另外注意的定义
例:

⑥ P63-64: 右线性文法转NFA
如图即可

⑦ P65:DFA转右线性文法
终结符T:字母表T
非终结符N:状态集Q
初始字符S:初始状态
生成式P:如下
此外,根据文法会不会有,可能结果会不一样,但是可以推出空串的往往更简洁
至此,3.8节及之前可以构建成系统的内容就概括完了
其他内容
暂 略
泵浦引理

例:
自动机的最小化:填表法

首先在终结状态和非终结状态的状态对应的格子里标X,他们显然可以区分。
其次,如果两个状态同时通过一个符号(比如a)可以走到一对可区分的状态上,那么也标上X。
如果他们走到的状态不是已知可区分的,就记录下来,直到填完整个标,如果还是不能断定他们可区分,那就是不可区分的,合为一个状态。注意,这个过程中,记录下来他们通过每一个符号(a、b、c……)走到的一对状态,其中任意一对可区分就认为他们也可区分
米兰机与摩尔机
下推自动机
- 最左/最右推导:每次将最左/右的非终结符进行一次推导
- 二义性:同一个字符串可以由两颗不同但边缘相同(从左到右叶子结点相同)的树得出
上下文无关文法CFL的变换
1、消除无用符号
- 找出有用非终结符:找出所有能直接或间接推出终结符串的非终结符作为有用符号
- 找出有用符号:找出所有从S直接或间接可达的符号(包括终结符和非终结符)作为有用符号
例:
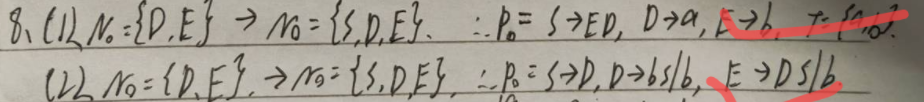
(注意,如第一题,C不能推出终结符,所以后面从S出发的时候,含有C的式子都直接扔掉)
2、消除生成式

即,若,则枚举ABC中可能为的元素为的情况。即,若ABC都有可能推出空,那就枚举均不为空、A为空、b为空……AB为空……ABC为空(如果都为空的情况下是就不写出来了)的8种情况
且,如果S也可以推出,就加入一个作为起始符,并特别写明它可以推出原S或
例:

3、消除单生成式

但是讲的不是很好用
速通:对于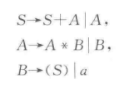 ,S可以推出A,是一个单生成式,那就把A带入,得到,现在S推出B还是,继续带入,得到
,S可以推出A,是一个单生成式,那就把A带入,得到,现在S推出B还是,继续带入,得到
对于循环的问题,如
S可以推出,它们也都可以再推出S。所以将S可以推出非终结符的集合记作,其中的非终结符的非单生成式结果才是S可以推出的结果(即如果里有单生成式,不填给S)
4、消除左递归
省流:
-
非终结符排序:若A推出的式子里,第一个符号有B,那B排在A的后面。下一步时先从最后面的开始变换,然后带回到前面的式子里再变换

-
 即,将原本的非左递归式取出来保留在A的生成式,然后将他们的每一个再写作,而A'是将原本左递归的一项变成两项:删除左递归的A,和将这个A移到后面 的两个生成式。
即:
即,将原本的非左递归式取出来保留在A的生成式,然后将他们的每一个再写作,而A'是将原本左递归的一项变成两项:删除左递归的A,和将这个A移到后面 的两个生成式。
即: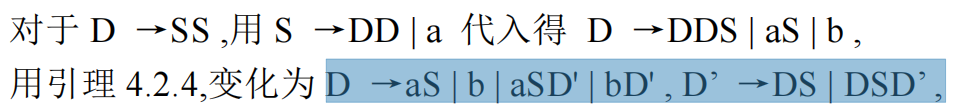
或

(A3A4A5不包含A2,所以和b同样地位处理)
使用顺序:先消,再消单生成式,再消无用符号
CNF范式的转换

用上面三步跑完,然后把长度大于2的生成式两个一分即可(注意,A推出aa这种式子要写成A推出BB,B推出a才行)
例:

GNF范式的转换

即,在前三个算法之后,再消除左递归,带入使其符合上面概念
下推自动机
定义


表示在状态q,读入a,栈顶为Z时,转成状态p,栈顶变为r。等价于的格局推导。

终态接受必然可以变成空栈接受
CFL转PDA

即,将每一个非终结符X推导出都写成一条边;将每个终结符都写一个可以抵消的转移边()。

或: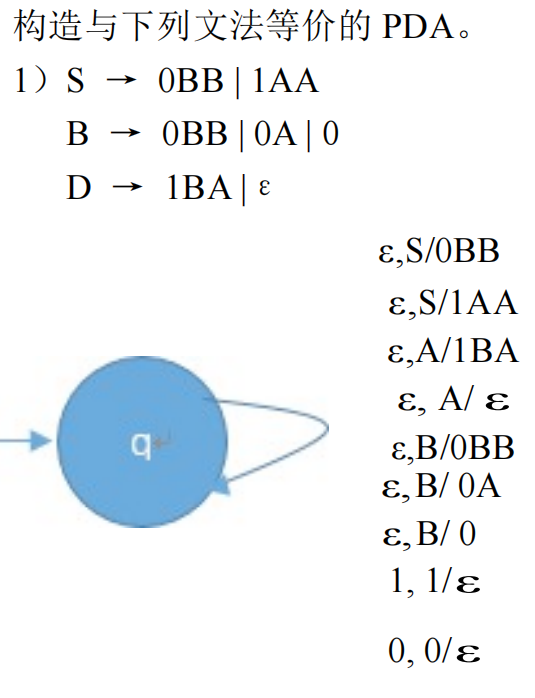
PDA的边,即:状态q到状态p的边上,,表示:。即状态q,读入a,栈顶就从B变为。
CFL的泵浦引理

- 取一常数p,构造一个特殊的语言L的字符串长度大于p,且可以切分,分出来的结果中,长度,非空
- 讨论的位置的情况,证明:存在一个特定的字符串中,在所有位置的情况都不能满足重复任意次仍属于语言L(或者无关位置的话就证明长度之类的,这种不用分类讨论)
例:
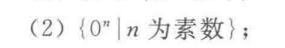


或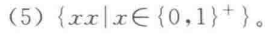

(这里关键是构造x为特殊的形态:,只要这一个不满足引理就可以说明他不是CFL了)
图灵机
定义
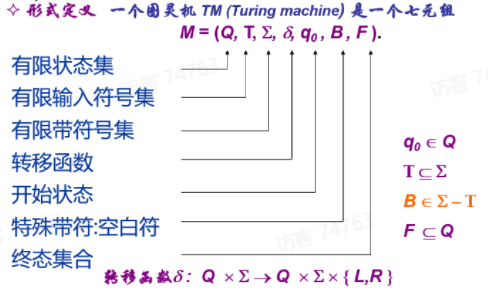
用描述图灵机的瞬间工作状态,表示读写头正扫描w2的最左字符

即表示读头如果在状态q时读到Xi,那么将Xi修改为Y,并且状态变为p,同时读头左移一格(R就是右移)
例题
1、
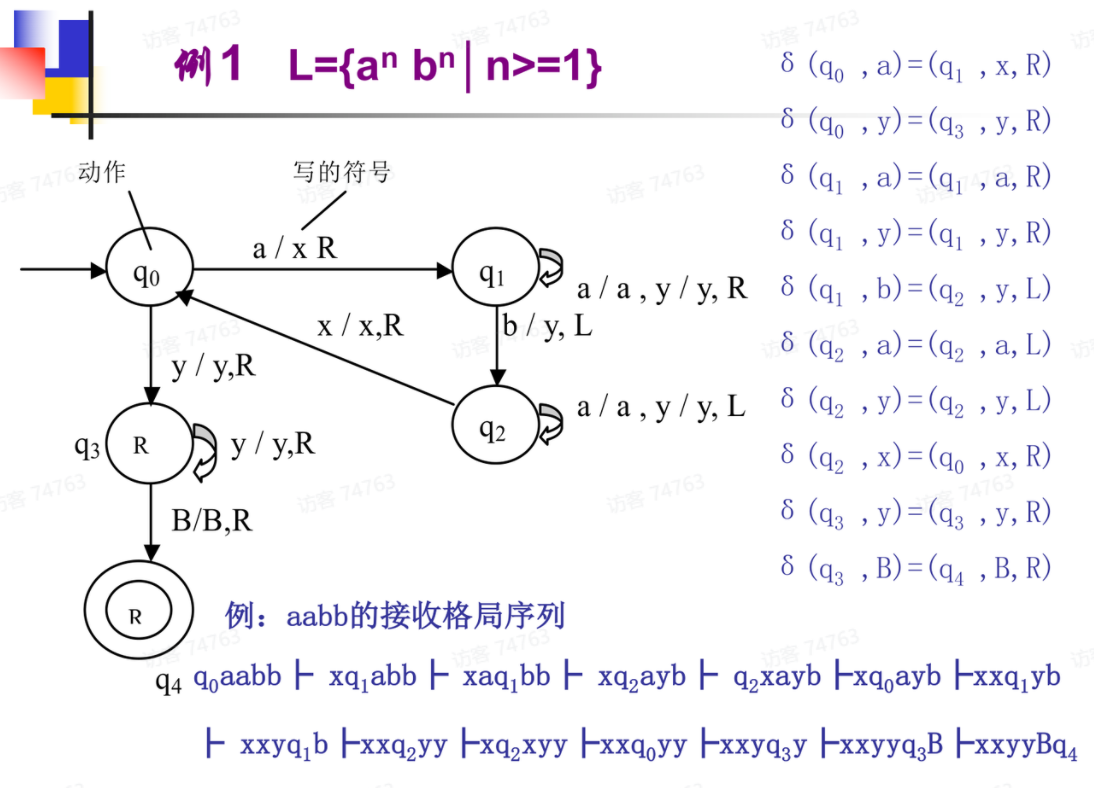
自动机图中,的边上写或表示“若读头在状态q0读入了a,就在a的地方写上X,然后右移一格,状态变为q1”,即
2、

对于这种,思想就是0读一个,改写为X;然后右移把1读一个,改写Y;然后右移把2读一个,改写Z;然后一直移到左边,读一个0,循环。最后没0了,就跑到最右边,看是不是B(即为空),是B就能接受(能停机)。