Relation Model

Relational Data Structure

We define a relation to be a subset of a Cartesian product of a list of domains.

Formally, given sets $D_{1}, D_{2}, \dots D_{n}$ , a relation $r$ is a subset of $D_{1} \times D_{2} \times \dots \times D_{n}$ Thus a relation is a set of n-tuples $(a_{1}, a_{2}, \dots, a_{n})$ where $a_{i} \in D_{i}$ .

And the difference here are :

Assign attribute name to every domain
Finite set

Relation Schema

$A_{1}, A_{2}, \dots, A_{n}$ are attributes, each attribute of a relation has a name, and $R = (A_{1}, A_{2}, \dots, A_{n})$ is a relation schema. $r (R)$ is a relation on the relation schema $R$ .

Relation Instance

The current values(a.k.a. relation instance) of a relation are specified by a table. An element $t$ of $r$ is a tuple, represented by a row in a table.

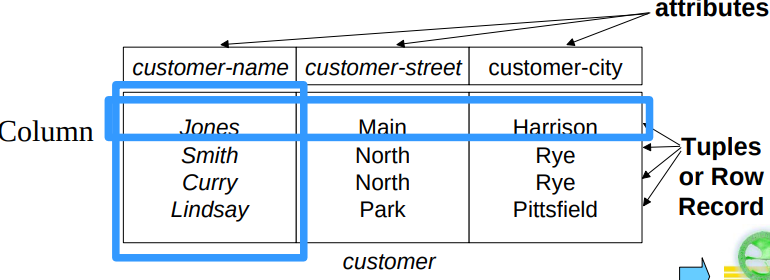
Order of tuples is irrelevant, tuples may be stored in an arbitrary order
Order of attributes is irrelevant
For all relations, the domains of all attributes be atomic
Attributes names must be different
Several attributes can have the same domain
Tuples are not duplicate

Super Key

$R (U)$ is a relation schema, $K$ is a super key for $R$ ,for any $r$ , no two distinct tuples have the same values on $K$ . That is, if $t_{1}$ and $t_{2}$ are in $r$ and $t_{1} \neq = t_{2}$ , then $t_{1} [K] \neq = t_{2} [K]$ . Values for $K$ are sufficient to identify a unique tuple of each possible relation $r (R)$ by "possible $r$ ".

A candidate key of en entity set is a minimal super key. Although several candidate keys may exist, one of the candidate keys is selected to be the primary key.

Candidate Key has two properties:

Uniqueness. No legal value of $R$ ever contains two distinct tuples with the same value for $K$
Irreducibility. No proper subset of $K$ has the uniqueness property.

Foreign Key

For $R_{1}$ , $R_{2}$ , $R_{1}$ includes the Primary Key $X$ of $R_{2}$ , $X$ is called a foreign key referencing $R_{2}$ . $R_{1}$ is called the referencing relation of the foreign key dependency. $R_{2}$ is called the referenced relation of the foreign key.

Integrity Constraint

Integrity constraint of primary key: each specified column of primary key is assumed to be not null.

Referential integrity constraint: the value of foreign key in any tuple of relation $R_{1}$ are either null or must appear as the value of primary key of a tuple of relation $R_{2}$ .

Fundamental Relational-Algebra-Operations

We have six basic operators:

Select
Project
Union
Set difference
Cartesian Product
Rename

Select

Notation $σ_{p} (r)$ , $p$ is called the selection predicate, defined as $σ_{p} (r) = {t ∣ t \in r an d p (t)}$ where $p$ is a formula in propositional calculus consisting of terms connected by $\lor$ and, $\land$ or , $\neg$ not.

Project

Notation: $Π_{A_{1}, A_{2}, ..., A_{k}} (r)$ where $A_{1}$ , $A_{2}$ are attribute names and $r$ is a relation name.

The result is defined as the relation of $k$ columns obtained by erasing the columns that are not listed. And the duplicate rows will be removed since relations are sets.

Union

Notation: $r \cup s = {t ∣ t \in ror t \in s}$ For $r \cup s$ to be valid:

$r$ and $s$ must have the same number of attribute
The attribute domains must be compatible
And the attribute name can be not the same

Set Difference

Notation: $r - s = {t ∣ t \in r an d t \in / s}$ For $r - s$ to be valid, the $r$ and $s$ has the same requirements with union operation.

Cartesian Product

Notation: $r \times s = {t q ∣ t \in r, q \in s}$ Combine information from $r$ and $s$ . Assume that there are $m$ relations in $r$ , $n$ relations in $s$ , there will be $m \times n$ in $r \times s$ ; Assume that $r$ has $a$ attributes and $s$ has $b$ attributes, there will be $a + b$ in $r \times s$

Rename

Allow us to rename and therefore to refer to the result of relational-algebra expressions. And allow use to refer to a relation by more than one name.

$ρ_{x} (E)$ returns the expression $E$ under the name of $X$ .

Additional Relational-Algebra-Operations

We define additional operations that do not add any power to the relation algebra but simplify common queries.

Set Intersection

Notation: $r \cap s = {t \in r an d t \in s}$ Having the same requirements with union operation.

And we have: $r \cap s = r - (r - s)$

Join

$r ⋈_{A ϑB} s = {t q ∣ t \in r an d q \in s an d t [A] ϑt [B]} = σ_{A ϑB} (r \times s)$

And the $ϑ$ is $ϑ \in {=, >, <, \neq =, \geq, \leq}$

Natural Join

Natural join is the default of join: $r ⋈ s = Π_{A tt r (r) \cup {B}} σ_{r . B = s . B} (r \times s)$ $B$ is the same attribute of $r$ and $s$ .

Outer Join

An extension of the join operation to avoid loss of information. Computes the join and then adds tuples from one relation that does not match tuples in other relation to the result of the join; use null value to fulfill the nonexistent attribute.

And there are three outer join:

Left outer join
Right outer join
Full outer join

Extended Relational-Algebra-Operations

Null Values

It is possible for tuples to have a null value denoted by null for some of their attributes.

Null signifies an unknown value or that a value does not exist. The result of any arithmetic expression involving null is null. Aggregate functions simply ignore null values. Duplicate elimination and grouping, null is treated like any other value and two null are assumed to be the same.

Comparisons with null values return the special truth value: unknown. And we can extend logic to three values with:

Unknown or true is true

Unknown or false is unknown

Unknown or Unknown is unknown
True and unknown is unknown

False and unknown is false

Unknown and Unknown is unknown
Not unknown is unknown

Ricardo's Wiki