字符串

串的概念和基本操作

基本概念

字符串：是由零个或者多个字符组成的有限序列。串是特殊的线性表，数据元素是单个字符。

子串和主串：串中任意个连续的字符组成的子序列称为该串的子串。包含子串的串称为主串
串相等：两个串的长度相等，且对应位置的字符都相等
空串和空白串：空串不包含任意的字符，用 $\emptyset$ 表示，空白串由一个或者多个空格组成
子串的位置：子串中第一个字符在主串中的序号称为子串的位置

串需要支持一系列的基本操作：

求串长
串赋值
串连接
串比较
求子串
子串定位

串的定长存储

方法一：顺序存储空间的第一个位置存放串中字符的个数

方法二：串后边再存放一个特殊字符\0表示结尾，\0不算做串中的元素

使用链式存储存储字符串的方式称作链串。使用链串有助于进行插入和删除的操作，但是空间的利用率比较低。

模式匹配

子串定位操作称为串的模式匹配。

模式匹配在计算机中的应用是非常广泛的，比如搜索引擎和在文档中搜索特定的单词。

简单模式匹配算法

方法：穷举法。

在主串中每次取出长度和子串相等的子串，将这两个子串相互比较，直到找到相同的子串或者比对结束。

int simpleIndex(string source, string target)
{
    int i = 0;
    int j = 0;

    while (i < source.length() and j < target.length())
    {
        if (source[i] == source[j])
        {
            // 匹配成功
            i++;
            j++;
        }
        else
        {
            i = i - j + 1;
            j = 0;

        }
    }

    if (j > target.length())
    {
        return i - target.length();
    }
    else
    {
        return -1;
    }
}

在设计这个算法中需要注意：

匹配失败后再次开始的位置
匹配成功的判断条件

但是在子串和主串的相似程度比较高的时候，这种匹配算法的复杂度就会比较高。在主串中可能存在大量和子串部分匹配的内容，算法中回溯的次数就会比较多。

模式匹配改进算法——KMP

算法主要改进在遍历时主串回溯这一问题，使在比对时指向主串中比对位置的指针不必回退。实现这一点的关键就是，在完成一个部分匹配之后，先对子串部分匹配的部分进行一个自匹配，因为此时子串部分匹配的部分和主串时相同的。

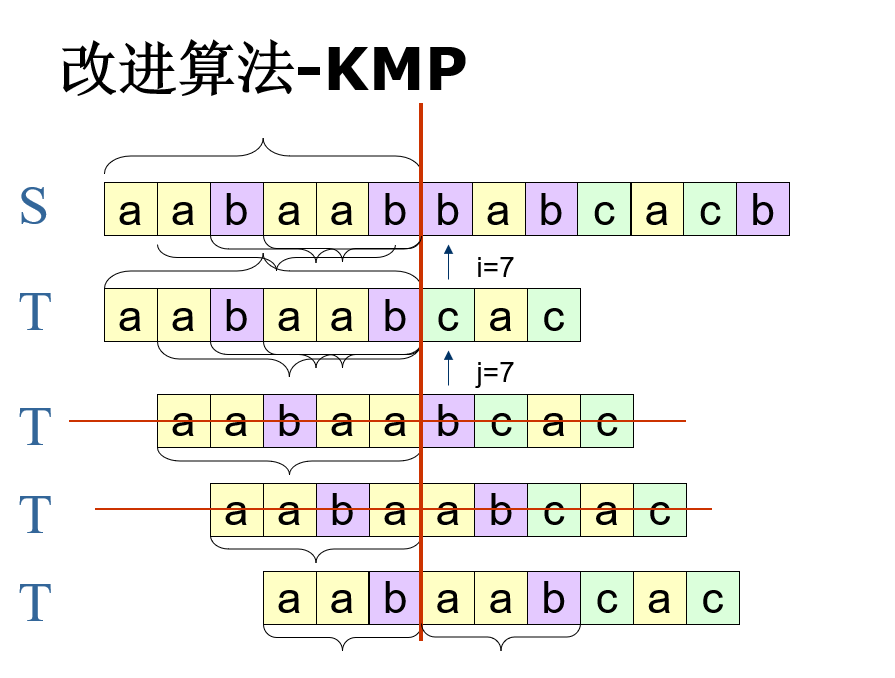
在设计实现KMP算法中主要的难点就是：如何确定已经部分匹配的子串应该向前滑动的长度？

由于确定这个长度和主串没有关系而只和子串有关系，我们可以先针对子串生成一个数组来存储当部分匹配到某一个位置之后，子串可以向后面滑动的长度。而且由于子串向后滑动等效于向前移动子串的开始匹配位置，我们可以先根据子串建立起一个当前匹配位置和下一次匹配位置的对应数组。

next数组

在kmp算法中比较重要的部分就是next数组的获得。next数组从定义来说是当前字符串的前缀和后缀最多匹配的位数。

字符串	next
a	0
ab	0
abb	0
abbc	0
abbca	1
abbcad	0
abbcada	1
abbcadab	2
abbcadabb	3

下面是通过通过模式串求得next数组的算法。

int getNext(int nextArray[], char str[], int length)
{
    int j = 0;
    int k = -1;

    nextArray[0] = -1;

    while(j < length)
    {
        if (k == -1 || str[j] == str[k])
        {
            j++;
            k++;
            nextArray[j] = k;
        }
        else
        {
            k = nextArray[k];
        }
    }
}

在获得了next数组之后，我们就可以简单的写出kmp算法的匹配部分。

int kmpMatch(char pattern[], char str[], int patternLength, int strLength)
{
    int nextArray[patternLength];

    getNext(nextArray, pattern, patternLength);

    int patternPos = 0;
    for(int pos = 0; pos < strLength; pos++)
    {
        if (pattern[patternPos] == str[pos])
        {
            patternPos++;
            pos++;

            if (patternPos == patternLength)
            {
                return pos;
            }
        }
        else
        {
            patternPos = nextArray[patternPos - 1];
        }
    }
}

‍

Ricardo's Wiki