Graph

Graph Terminology

We will learn the following terms:

Adjacent
connect
endpoint
neighborhood
degree
initial
terminal
in-degree
out-degree
complete
cycles
wheels
n-cubes
bipartite
subgraph
union

Graph Representation & Isomorphism

Connectivity

Path

In a undirected graph, a path of length $n$ from $u$ to $v$ is a sequence of adjacent edges going from vertex $u$ to $v$ .

A path is a circuit , or close walk, if $u = v$
A path traverses then vertices along it
A path is simple if it contains no edge more than once. When a path is simple, we can denote this path by these vertices sequence $x_{0}, x_{1}, \dots, x_{n}$

Path in Directed Graphs

Same as in undirected graphs, but the path must go in the direction of the arrows.

When there are no multiple edged in the directed graph, this path is denoted by its vertices sequence same as that in undirected graph
A path of length greater than zero and begins and ends at the same vertex is called a circuit or cycle

An undirected graphs is connected if there is a path between every pair of distinct vertices in the graph. An undirected graph that is not connected is called disconnected. We say that we disconnect a graph when we remove vertices or edges, or both, to produce disconnected subgraph.

Theorem: There is a simple path between any pair of vertices in a connected undirected graph.

Cut Vertices & Cut Edge

We call a connected graph is a connected component

The removal from a graph of a vertex and all incident edges produces a subgraph with more connected components. Such vertices are called cut vertices or articulation points.
An edge whose removal produces a graph with more connected components than in the original graph is called a cut edge or bridge.
A cut vertex or cut edge separates 1 connected component into 2 if removed.

Vertex Connectivity & Edge Connectivity

Connected graphs without cut vertices are called nonseparable graphs, and can be thought of as more connected than those with a cut vertex.

A subset $V^{'}$ of the vertex set $V$ of $G = (V, E)$ is a vertex cut, or separating set, if $G - V^{'}$ is disconnected. We define the vertex connectivity of a noncomplete graph $G$ as the minimum number of vertices in a vertex cut, denoted by $K (G)$ . The larger $K (G)$ is, the more connected we consider $G$ to be. A graph is k-connected, if $K (G) \geq k$ .

Same as vertex connectivity, we can define the edge connectivity. A set of edges $E^{'}$ is called an edge cut of $G$ if the subgraph $G - E^{'}$ is disconnected. The edge connectivity $λ$ of a graph $G$ , denoted by $λ (G)$ , is the minimum number of edges in an edge cut of $G$ .

And we have $K (G) \leq λ (G) \leq min {d e g (v), v \in V}$

Directed Connectedness

A directed graph is strongly connected if there is a directed path from $a$ to $b$ for any two vertices $a$ and $b$ .

That means there is path from $a$ to $b$ and also a path from $b$ to $a$

It is weakly connected if and only if the underlying undirected graph is connected. And we can get strongly implies weakly but not vice-verse.

Counting Paths using Adjacency Matrices

Let $A$ be the adjacency Matrices of graph $G$ . The number of different paths of length $r$ from $v_{i}$ to $v_{j}$ , where $r$ is a positive integer,equals the $(i, j)$ th entry of $A^{r}$ .

Paths & Isomorphism

The connectedness and the existence of a circuit or simple circuit of length $k$ are graph invariants with respect to isomorphism.

Euler and Hamilton Paths

LEAD-IN: Bridges of Königsberg Problem七桥问题

Eulerian Graph

An Euler Circuit in a graph $G$ is a simple circuit containing every edge of $G$ .

An Euler Path in $G$ is a simple path containing every edge of $G$ .

An Euler Tour is a a walk in a graph if it starts and ends in the same place and uses each edge exactly once.

An Euler Trail is a walk in a graph if it uses each edge exactly once.

A connected graph $G$ is Eulerian when it has at least two vertices has an Euler circuit. And a graph is Eulerian if and only if G is connected and has no vertices of odd degree.

A connected graph $G$ has an Euler trail from node $a$ to some other node $b$ if and only if $G$ is connected and $a \neq = b$ are the only two nodes of odd degrees.

Constructing Euler Circuit Algorithm

procedure Euler(G: connected multigraph with all vertices of even degree)
circuit := a circuit in G begining at an arbitrarily chosen vertex with edges
        successively added to form a path that returns to this vertex
H := G whith the edges of this circuit removed
while H has edges:
        subcircuit := a circuit in H beginning at a vertex in H that also is an
                endpoint of an edge of circuit
        H := H with edges of subcircuit and all isolated vertices removed
        circuit := circuit with subcircuit inserted at the appropriate vertex
return circuit {circuit is an Euler circuit}

Hamilton Graph

A graph has a Hamiltonian tour if there is a tour that visits every vertex exactly once (and returns to its starting point).

A graph with a Hamiltonian tour is called a Hamiltonian graph.

A Hamiltonian path is a path that contains each vertex exactly once.

A Hamiltonian circuit is a circuit that traverses each vertex in $G$ exactly once.

At this time, we don't have nice characterization of Hamiltonian graphs the way there was with Eulerian graphs. But we have some experience in this area. For example, there are some properties imply a graph not a Hamilton, such as (1) vertex with degree 1, (2) vertex with two degrees must be in the circuit. When a circuit is being constructed and this circuit has passed through a vertex, then all remaining edges incident with this vertex, other than the two used circuit, can be removed from consideration. And a Hamilton circuit can't contain a smaller circuit within it.

Hamiltonian Path Theorems

Dirac's Theorem: If $G$ is connected, simple, has $n \geq 3$ vertices, and $\forall v d e g (v) \geq \frac{n}{2}$ , then $G$ has a Hamiltonian circuit.
Ore's Corollary: If $G$ is connected, simple, has $n \geq 3$ nodes, and $d e g (u) + d e g (v) \geq n$ for every pair $u, v$ of non-adjacent nodes, then $G$ has a Hamiltonian circuit.

Shortest Path Problems

Introduction

A weight graph is one in which weight are assigned to all edges connecting each two vertices.
Such number may have different meanings, such as instance, travelling distance, monthly cost or travelling time between two vertices.
The length of a path in a weight graph is the sum of the weights of the edges of this path. This length is different from the number of edges in a path in a graph without weights.

Shortest Path Algorithm

Powered by Dijkstra

起始点的路径标为0，其他路径标为无穷大，在后续遍历中更新
定义一个已经标好最短路径的点的集合S
将最短路径的点放进去
从新放入的店开始，寻找其他点的最短路径
重复3~4，直到达到路径的目标

Dijkstra's Algorithm Complexity

Dijkstra's algorithm finds the length of a shortest path between two vertices in a connected simple undirected and weighted graph.
Dijkstra's algorithm uses $O (n^{2})$ operations(additions and comparisons) to find.

Determining the shortest path from $a$ to an assigned vertex
Determining the shortest path of any two vertices in the graph

Finding the shortest path between any two vertices using distance matrix

Distance Matrix: Let G is a graph with n vertices. The distance matrix of G is $D = (d_{ij})_{n \times n}$

$d_{ij}$ represent the weights of the edges $(v_{i}, v_{j})$
If there is no edge between $v_{i}$ and $v_{j}$ then $d_{ij} = \infty$
$d_{ij}^{2}$ is the shortest length of the path from $v_{i}$ to $v_{j}$ with two edges
$d_{ij}^{k}$ is the shortest length of the path from $v_{i}$ to $v_{j}$ with $k$ edges

To get the shortest length of path, we define $\oplus$ : Let $A = (a_{ij})_{n \times n}$ and $B = (b_{ij})_{n \times n}$ , and $C = A \oplus B$ , where $c_{ij} = min (a_{ij}, b_{ij})$ .

So we can define $P = D \oplus D^{2} \oplus D^{3} \oplus \dots \oplus D^{n}$ , and in such matrix, $p_{ij}$ represent the shortest length from $v_{i}$ to $v_{j}$ .

Travelling Salesperson Problem

In an undirected simple weighted graph, we need to find the shortest length of Hamilton path.

This is a NP problem

Planar Graph

Definition

A graph is called planar if it can be drawn in the plane in such way that no two edges cross.

A planar representation of a graph splits the plane into regions that we call it faces, including an unbound region.

Euler Theorem

Let $G$ be a connected planar simple graph with $e$ edges , $v$ vertices. Let $r$ be the number of regions in a planar representation of $G$ , then we have $r = e - v + 2$

We can prove this theorem by mathematical induction. Constructing a sequence of subgraphs $G_{1}, G_{2}, \dots, G_{n}$ successively adding an edge at each stage.

Basic step: G have no cycle, so $e_{1} = 1$ , $v_{1} = 2$ , $r_{1} = 1$
Inductive step: there are two ways to add an edge:
- Adding an edge by connecting two existing vertices, which add a new region
- Adding a new vertex and connect it with graph, which keeps region unchanged

Corollary

No matter how we redraw a planar graph it will have the same number of region
Every simple $n$ -node ( $n \geq 3$ ) planar graph $G$ has at most $3 n - 6$ edges.
If $G$ a connected planar simple graph, then $G$ has a vertex of degree not exceeding five.

The main idea in proof: Every face has at least 3 edges no its boundary. Every edge lies on the boundary of at most 2 faces Thus $2 e \geq 3 r$
If a connected planar simple graph has $e$ edges and $n$ vertices with $n \geq 3$ and no circuit of length three, then $e \leq 2 n - 4$

Kuratowski Theorem

Kuratowski Graph

Kuratowski graphs are two typically non-planar graphs.

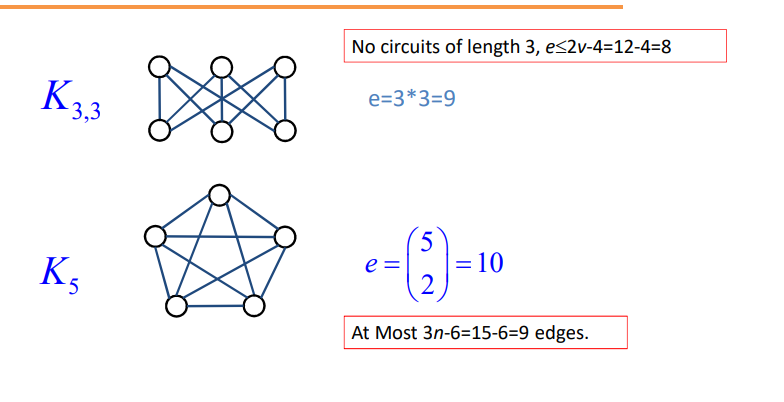
In the Kuratowski graph, we can find that:

If we replace edges in a Kuratowski graph by paths of whatever length, they remain non-replace.
If a graph contains a subgraph obtained by starting with $K_{5}$ or $K_{3, 3}$ and replacing edges with paths, then $G$ is non-planar.

Homeomorphic Graph

If a graph is planar, so will be any graph obtained by removing an edge ${u, v}$ and adding a new vertex $w$ with edges ${u, w}$ and ${w, v}$ . Such an operation is called an elementary subdivision .

The graphs are called homeomorphic if they are obtained from the same graph by a sequence of elementary subdivisions.

Kuratowski Theorem

A graph is planar if and only if it contains no subgraph obtained from $K_{5}$ or $K_{3, 3}$ by replacing edges with paths.

Graph Coloring

Lead in: four colors are always enough to color any map drawn on a plane.

Coloring graphs

Suppose that $G = (V, E . γ)$ is a graph without no multiple edges, and $C = c_{1}, c_{2}, c_{3}, \dots$ is any set of $n$ colors. Any function $f : V \to C$ is called a coloring of the graph $G$ using $n$ colors.

A coloring is proper if any two adjacent vertices $v$ and $u$ have different colors. The smallest number of colors needed to produce a proper coloring of a graph $G$ is called the chromatic number of $G$ , which is denoted by $χ (G)$ .

Four-color Theorem

The vertices of ant planar graph can be 4-colored in such a way that no two adjacent vertices receive the same color.

This is hard to prove.

Five-Color Theorem

Any planar graph can be colored with five colors.

Prove

Let $G$ be a node-minimal counter-example to the theorem, for example, a planar graph that requires 6 colros.

As $G$ is a planar graph, we can get $G$ must have a node $q$ with degree $\leq 5$ . Let the nodes adjacent to q be named as $v_{1}, v_{2}, v_{3}, v_{4}, v_{5}$ , and this five nodes can not form $K_{5}$ , also because this is a planar graph. So there must be two vertices $a_{1}, a_{2}$ in this five vertices that have no edge between them.

So we can "contract" the edges $< q, v_{1} >$ and $< a, v_{2} >$ to get a new planar graph $G^{'}$ , and the vertices $v_{1}$ , $v_{2}$ and $q$ become a new vertices in $G^{'}$ . $G^{'}$ is 5 colorable since it has fewer nodes than $G$ , so we can find that we color the $G$ using the five colors in the $G^{'}$ , which meaning the counter example is not counter.

Applications of Graph Coloring

Fifteen different foods are to be held in refrigerated compartments within the same refrigator.
How can the final exams be scheduled at a university so that no students has two exams at the same time.
Frequency assignment. we need to assign different radio frequency to two radio station whose distance is to short.

Chromatic Polynomials

If $G$ is a graph and $n \geq 0$ is an integer, let $P_{G} (n)$ be the number of ways to color $G$ properly using $n$ or fewer colors. $P_{G} (n)$ is called the chromatic polynomials. And if we can find the chromatic polynomials ,we can easily get the chromatic number of $G$ .

For example, for a linear graph $L_{4}$ , we have the chromatic polynomials $x (x - 1)^{3}$ , so $P_{L_{4}} (0) = 0$ , $P_{L_{4}} (1) = 0$ and $P_{L_{4}} (2) = 2$ , so $χ (L_{4}) = 2$ .

Theorem 1

If $G$ is disconnected graph with components $G_{1}, G_{2}, G_{3}, \dots, G_{m}$ , then $P_{G} (x)$ is the product of the chromatic polynomials for each components.

$P_{G} (x) = P_{G_{1}} (x) P_{G_{2}} (x) \dots P_{G_{m}} (x)$

Subgraph and Quotient Graphs

One of the most important subgraphs is the one that arises by deleting one edge and no vertices. If $G = (V, E, γ)$ is a graph and $e \in E$ , then we denote by $G_{e}$ the subgraph obtained by omitting the edge $e$ from $E$ and keeping all vertices.

Suppose that $G = (V, E, γ)$ is a graph without multiple edges between the same vertices and that $R$ is an equivalence relation on the set $V$ . Construct the quotient graphs $G^{R}$ as follow: The vertices of $G^{R}$ are the equivalence classes of $V$ produced by $R$ . If $[v]$ and $[w]$ are the equivalence classes of vertices $v$ and $w$ , then there is an edge in $G^{R}$ from $[v]$ to $[w]$ if and only if some vertices in $[v]$ is connected to sone vertices in $[w]$ in the graph $G$ .

Theorem 2

Let $G = (E, V, γ)$ be a graph without multiple edges, and let $e \in e$ , say $e = {a, b}$ . So we have $G_{e}$ , subgraph obtained by deleting $e$ and $G^{e}$ , the quotient graph of $G$ obtained by merging the end points of $e$ . And then with $x$ colors:

$P_{G} (x) = P_{G_{e}} (x) - P_{G^{e}} (x)$

Transport Networks

An important use of labeled graph is to model what are commonly called transport networks. The label on an edge represents the maximum flow that can be passed through that edge and is called the capacity of the edge.

Transport Network

A transport network, or a network, is a connected digraph $N$ with the following properties:

There is a unique node, the source, that has in-degree 0. We always label the source with node 1.
There is a unique node, the sink, that has out-degree 0. If $N$ has n nodes, and we always label the sink with node n.
The graph $N$ is labeled. The label, $C_{ij}$ , on edge $(i, j)$ is a nonnegative number called the capacity of the edge.

Flow

A flow in a network is a function that assigns to each edge $(i, j)$ of $N$ a nonnegative number $F_{ij}$ that does not exceed $C_{ij}$ .

And when talking about flow, we have:

Conservation of flow
Value of flow

For any network, an important question is to determine the maximum value of a flow through the network and to describe a flow that has the maximum value.

Although edge $(j, i)$ is not in $N$ , there is no harm in consideration such a virtual flow as long as it only has effect of reducing the existing flow in the actual edge $(i, j$ )

Labeling Algorithm

Let $N$ be a network with $n$ nodes and $G$ be the symmetric closure of $N$ . All edges and paths used are in $G$ .

Begin with all flows set to 0.
As we proceed, it will be convenient to track the excess capacities in the edges and how they change rather than tracking the increasing flows.
When the algorithm terminates, it is easy to find the maximum flow from the final excess capacities.

STEP 1

Let $N_{1}$ be the set of all nodes connected to the source by an edge with positive excess capacities.
Label each node $N_{j}$ in $N_{1}$ with $[E_{j}, 1]$ , where $E_{j}$ is the excess capacity $e_{ij}$ of edge $(1, j)$ . The 1 in the label indicates that $j$ is connected to the source, node 1.

STEP 2

Let node $j$ in $N_{1}$ be the node with the smallest node number and let $N_{2} (j)$ be the set of all unlabeled nodes,

other than the source and those are joined to node $j$ and have positive excess capacity.
Suppose that node $k$ is in $N_{2} (j)$ and $(j, k)$ is the edge with positive excess capacity. Label node $k$ with $[E_{k}, j]$ , where $E_{k}$ is the minimum of $E_{j}$ and the excess capacity $e_{jk}$ of edge $(j, k)$ .
When all the nodes in $N_{2} (j)$ are all labeled in this way, repeat this process for the other nodes in $N_{1}$ . Let

$N_{2} = U_{j \in N_{1}} N_{2} (j)$

STEP 3

Repeat Step 2 , labeling all previously unlabeled nodes $N_{3}$ that can be reached from a node in $N_{2}$ by an edge having positive excess capacity.
Continue this process forming sets $N_{4}$ , $N_{5}$ , ... until after a finite number or steps
either the sink has not been labeled and no other nodes can be labeled. It can happened that no nodes have been labeled; remember that the source is not labeled or the sink has been reached.

In this case, the algorithm terminates and the total flow is a maximum flow.
or the sink has been labeled.

In this case, the sink has been labeled with $[E_{n}, m]$ where $E_{n}$ is the amount of extra flow that can be made to reach the sink through the path.

STEP 4

We examine the path in reverse:

If edge $(i, j) \in N$ , we increase the flow in $(i, j)$ and decrease the excess capacity $e_{ij}$ by the sam amount. Simultaneously, we increase excess capacity of the virtual edge $(i . j)$
If on the other hand , edge $(i, j) \neq \in N$ , we decrease the flow in $(j, i)$ and increase its excess capacity. Same as before, decrease the excess capcaity in $(i . j)$ .

Back to the step 1.

What a complex algorithm!

Cut

A cut in a network is a set $K$ of edges having the property that every path from the source to the sink contains at least one edge from $K$ .

The capacity of a cut $K$ is the sum of the capacities of all edges in $K$ . If $F$ is any flow and $K$ is any cut, there must be $v a l u e (F) \leq c (K)$ .

And we have a theorem that a maximum flow $F$ in a network has value equal to the capacity of a minimum cut of the network.

Super Source & Super Sink

When we meet a network with sources or sinks more than one, we can add a virtual source or virtual sink to use the labeling algorithm, which is connected with the real source and sink with large enough edge. These virtual source and sink is are called super source and super sink.

‍

Ricardo's Wiki