Advanced Counting Techniques

Example: How many bit string of length $n$ do not contain two consecutive zeros?

To solve this problem, let $a_n$ be the number of such strings of length $n$. An argument can be given that show that the sequence $\{a_n\}$ satisifies the recurrence relation $a_{n+1}=a_n+a_{n-1}$ and the initial condition $a_1=2$ and $a_2=3$.

Review of the definition of recurrence relation

A recurrence relation for a sequence $\{a_n\}$ is an equation that expresses $a_n$ in terms of one or more previous elements of the sequence, for all $n\ge n_0$.

A particular sequence, described non-recurisely, is said to solve the given recurrence relation if it is consistent with the definition of the recurence.

A given recurrence relation may have many solutions.

Some Examples

The Tower of Hanoi

​​

Let $H_n$ represent the number of moves for a stack of $n$ disks.

And we will have such a strategy:

• Move the top $n-1$ disks to spare peg, which is $H_{n-1}$​
• Move the bottom disk, 1
• Move the top $n-1$ disks to target reg, alos $H_{n-1}$​

So we will have $H_n=2H_{n-1}+1$

And $H_n=2^n-1$.

The Number of Bit String

Find a recurence relation and give initial conditions for the number of bits strings of length $n$ that do not have two consecutive 0s. How many such bit strings are there of length five?

Let $a_n$ denote the number of bit strings of lenght $n$;

$a_1=2$,as 0 and 1;

$a_2=3$, as 01, 10 and 11;

and we have the two ways to construct the $a_n$ bit string, add $1$ to $a_{n-1}$ and add $10$ to $a_{n-2}$, so we get the recurrence realtion $a_n=a_{n-1}+a_{n-2}$.

Catalan Numbers

Find a recurrence relation for $C_n$, the number of ways to parenthesize the product of $n+1$ numbers $x_0,x_1,x_2,x_3,\cdots ,x_n$ to specify the order of multiplication. For example $C_3=5$ since there are five ways to parenthesize $x_0,x_1,x_2,x_3$ to determine the order of multiplication: $((x_0\ast x_1)\ast x_2)\ast x_3$, $(x_0\ast (x_1\ast x_2)\ast x_3)$,$(x_0\ast x_1)\ast (x_2\ast x_3)$, $x_0\ast ((x_1\ast x_2)\ast x_3)$, $x_0\ast (x_1\ast (x_2\ast x_3))$.

$$\begin{array}{rl}{C}_n& =C_0{C}_{n_1}+C_1{C}_{n-2}+\cdots +C_{n-1}{C}_0\\ & =\sum _{k=0}^{n-1}{C}_k{C}_{n-k-1}\end{array}$$

Solving Recurrences

A linear homogeneous recurrence of degree $k$ wih constant coefficients , a.k.a k-LiHoReCoCo, is a recurence of the form

$$a_n=c_1{a}_{n-1}+\cdots +c_k{a}_{n-k}$$

where the $c_i$ are all real and $c_k\ne 0$.

The solution is uniquely determined if $k$ initial conitions are provided.

Solving LiHoReCoCos

Basic idea: look for solutions of the form $a_n=r^n$, where $r$ is a constant.

This requires the characterisitic equation:

$$\begin{gathered} r^n=c_1{r}^{n-1}+\cdots +c_k{r}^{n-k} \\ {r}^k-c_1{r}^{k-1}-c_{k-1}r-c_k=0 \end{gathered}$$

The solutions, called as characteristic roots, can yield an explicit formula for the sequence.

Consider an arbitary 2-LiHoReCoCos:

$$a_n=c_1{a}_{n-1}+c_2{a}_{n-2}$$

It has the characteristic equation:

$$r^2-c_{1}r-c_2=0$$

Theorem 1

If this CE has 2 roots $r_1\ne r_2$, then $a_n={\alpha }_1{r}_1^n+{\alpha }_2{r}_2^n$ for $n\ge 0$ for some constants ${\alpha }_1$ and ${\alpha }_2$.

Theorem 2

If this CE has only 1 root $r_0$, then $a_n={\alpha }_1{r}_0^n+{\alpha }_{2}n{r}_0^n$, for all $n\ge 0$, for some constants ${\alpha }_1$ and ${\alpha }_2$.

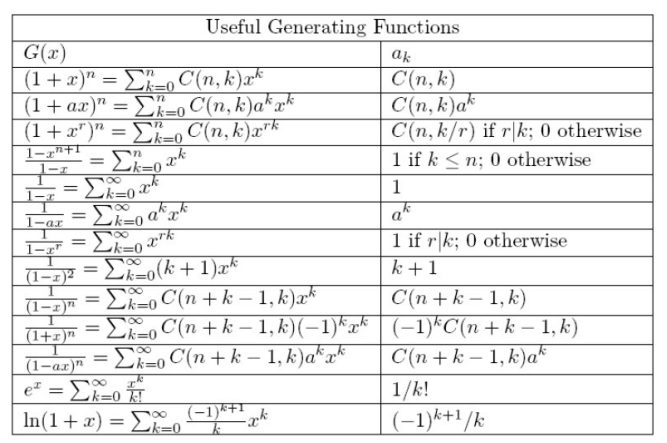
Generating Functions

The generating function for the sequence $\{a_n\}$ is the infinite power series

$$\begin{gathered} G(x)=a_0+a_{1}x+\cdots +a_n{x}^n+\dots \\ =\sum _{k=0}^{\infty }{a}_k{x}^k \end{gathered}$$

Theroem 1

Let $f(x)={\sum }_{k=0}^n{a}_k{x}^k$ and $g(x)={\sum }_{k=0}^n{b}_k{x}^k$, and we have:

• $f(x)+g(x)={\sum }_{k=0}^n(a_k+b_k)x^k$
• $f(x)g(x)={\sum }_{k=0}^n({\sum }_{j=0}^k{a}_j{b}_{k-j})x^k$

Extended Binomail Coefficient

Let $u\in R$ and $k\in Z^{+}\cup \{0\}$, the extended binomail coeffcient ${(}_k^n)$ is defined by

​​

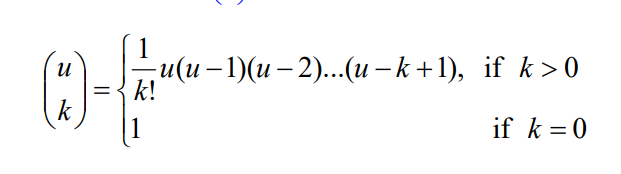
Extended Binomail Theroem

Let $x\in R$ and let $u\in R$, then

$$(1+x{)}^u=\sum _{k=0}^{\infty }{(}_k^n)x^k$$

As we have two theroems about generating functions, we give a list of some generating functions:

​​

‍