算法导论

算法

算法是指解决问题的一种方法或者一个过程。

算法是若干指令的有穷序列：

• 输入
• 输出
• 确定性
• 有限性

算法的时间复杂度分析

渐进性原理及表示符号

使用渐进性原理对于算法的时间复杂度进行分析，反映算法的时间复杂度随着$N$变化发生变化的情况，衡量了算法的规模。

使用渐进分析的专用记号对于渐进性进行分析：

• 渐进上界记号$O$
• 渐进下界记号$\Omega$
• 非紧上界记号$o$
• 非紧下界记号$\omega$
• 紧渐进界记号$\Theta$

渐进分析中中的符号类似于比较：

• $f(n)=O(g(n))\approx a\le b$
• $f(n)=\Omega (g(n))\approx a\ge b$
• $f(n)=\Theta (g(n))\approx a=b$
• $f(n)=o(g(n))\approx a<b$
• $f(n)=\omega (g(n))\approx a>b$

同时渐进分析记号还具有若干性质：

1. 传递性

2. 反身性

3. 对称性

4. 互对称性

5. 支持算术运算

   $O(f(n)+g(n))=O(max\{f(n),g(n)\})$

   $O(f(n))+O(g(n))=O(f(n)+g(n))$

   $O(f(n))\times O(g(n))=O(f(n)\times g(n))$

   $O(cf(n))=O(f(n))$

在算法中存在这些常见的复杂性函数：

对于小规模的数据，这些复杂性函数的图像：

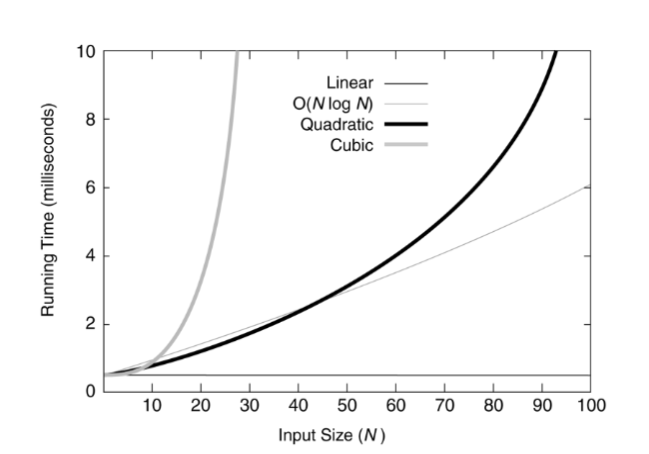
对于较大规模的数据，则图像为：

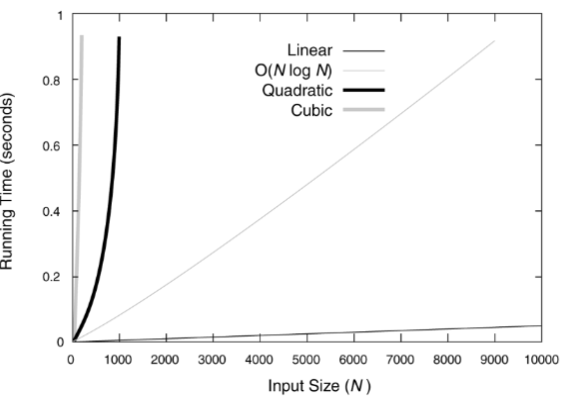
递归方程渐进阶的求解

代入法

先推测递归方法的显式解，然后使用数学归纳法证明这一推测的正确性。

例： 求证$T(N)=2T(\lfloor \frac{N}{2}\rfloor )+n$的渐进阶。

首先，推测$T(N)=O(nlogn)$， 即存在正的常数$C$和自然数$n_0$，使得当$n\ge n_0$时： $$T(N)\le Cnlogn$$ 假设当$2^{k-1}{n}_o\le n\le 2^k{n}_0$，$k>1$是，上面的推论成立，那么当$2^k{n}_0\le n\le 2^{k+1}{n}_0$时，有： \[ \begin{eqnarray} T(n) &=& 2T(\lfloor \frac{n}{2} \rfloor) + n \ &\le& 2 C \lfloor \frac{n}{2} \rfloor log(\lfloor \frac{n}{2} \rfloor) + n \ &<& 2C\frac{n}{2} log(\frac{n}{2}) + n \ &=& Cnlogn - Cn + n \ &=& Cnlogn - (c-1)n \ &\le& Cnlogn \end{eqnarray} \] 原假设成立。

迭代法

迭代展开递归方程的右端，使之成为一个非递归的合式，然后通过对合式的估计来达到对于方程左端解的估计。

例：求 $$T(n)=\{\begin{array}{l}7,n=1\\ 2T(\frac{n}{2})+5n^2,n>1\end{array}$$ 的渐进阶。 \[ \begin{eqnarray} T(n) &=& 2T(\frac{n}{2}) + 5n^2 \ &=& 2(2T(\frac{n}{4}) + 5(\frac{n}{2}))^2 + 5n^2 \ &=& 2(2(2T(\frac{n}{8}) + 5 (\frac{n}{4}) ^ 2) + 5(\frac{n}{2}))^2 + 5n^2 \ &=& 2^kT(1) + 2^{k-1} 5(\frac{n}{2^{k-1}}) ^ 2 + \cdots + 2 \times 5 (\frac{n}{2})^2 + 5n^2 \end{eqnarray} \] 不难发现： $$T(n)=O(n^2)$$ 迭代法还有一个衍生的方法——递归树法：

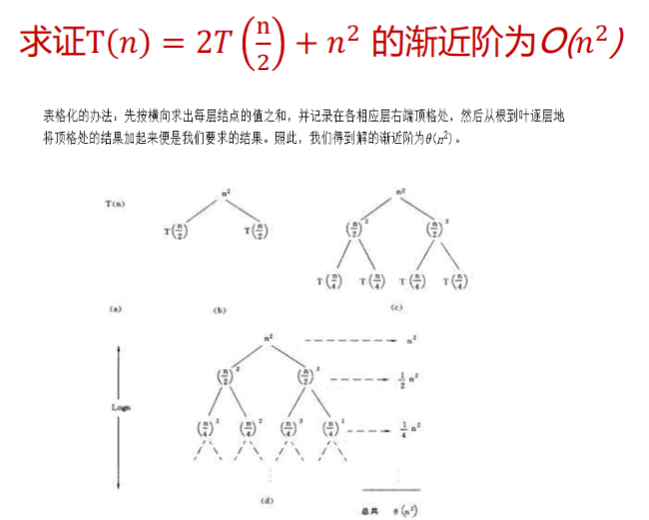
实际上就是使用树的方式表示整个递推公式。

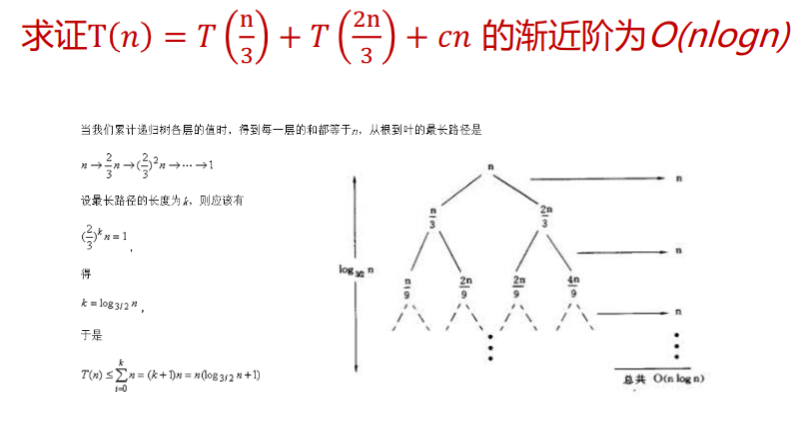
套用公式法

针对如下的递推方程 $$T(n)=\{\begin{array}{l}c,n=1\\ aT(\frac{n}{b})+c{n}^k,n>1\end{array}$$ 我们有 $$T(n)=\{\begin{array}{l}O(n^{lo{g}_b^a}),a>b^k\\ O(n^{k}lo{g}_{b}n),a=b^k\\ O(n^k),a<b^k\end{array}$$ 这个公式还有一般化的情况：

如果递归方程的形式为： $$T(n)=\{\begin{array}{l}c,n=1\\ aT(\frac{n}{b})+f(n),n>1\end{array}$$ 则针对$f(n)$进行讨论：

1. 如果$\exists ϵ>0$, 使得$f(n)=O(n^{lo{g}_{b}a-ϵ})$，那么我们有 $$T(n)=\theta (n^{lo{g}_{b}a})$$

2. 如果$f(n)=\theta (n^{lo{g}_{b}a})$，那么我们有 $$T(n)=\theta (n^{lo{g}_{b}a}\cdot logn)$$

3. 如果$\exists ϵ>0$，使得$f(n)=\Omega (n^{lo{g}_b(a+ϵ)})$，且当$\exists c<1$时，当$n$充分大时有$af(\frac{n}{b})\le cf(n)$，那么我们有 $$T(n)=\theta (f(n))$$

母函数法

通用的方法总是复杂的。

设$a_0,a_1,\cdots ,a_n$是任意的数列，那么称下面这个函数为数列的母函数： $$f(x)=a_0+a_{1}x+\cdots +a_n{x}^n$$ 如果数列是算法的复杂性函数$\{T(n)\}$，则其母函数为： $$f(x)=T(0)+T(1)x+\cdots +T(n)x^n$$ 如果能由$T(n)$也就是的数列的递归方程求出母函数，那么其第$n$项系数为$T(n)$。